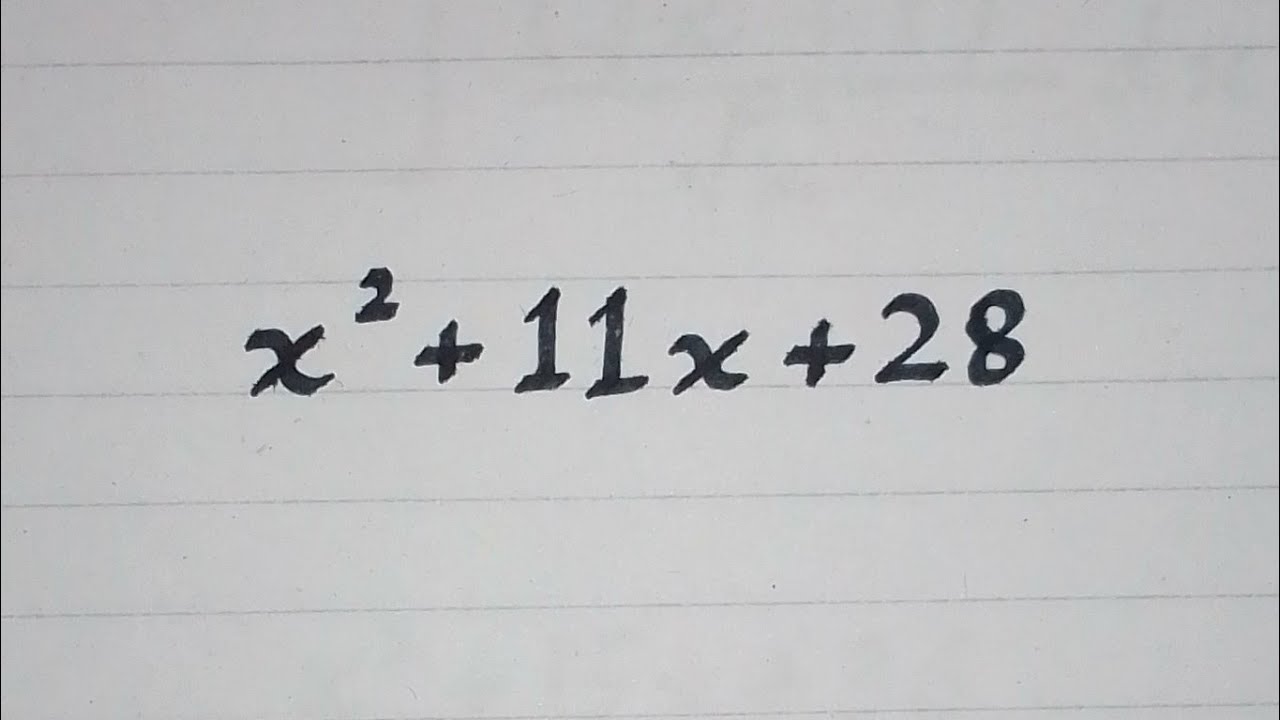Solving − x2-11x+28=0 | Quadratic Equation

Quadratic equations are pivotal in algebra, offering insights into various phenomena across disciplines such as physics, astronomy, economics, and even biology. The equation ${}^{}$ is a classic example, embodying the quintessential properties of quadratic forms. Its analysis not only enlightens us about specific solutions but also reveals broader mathematical concepts.

Structure and Characteristics of Equation x2-11x+28=0

This quadratic equation falls under the standard form $$, where $$, $$, and $$ are real numbers, and $\mathrm{a\; \ne }0$. In ${}^{}$x2-11x+28=0:

• $\mathrm{}$, showing the equation is a simple quadratic without a leading coefficient.$$
• $\mathrm{}$, indicating the linear term’s influence on the curve’s shift and orientation.
• $\mathrm{}$, the constant, affects the vertical translation of the quadratic graph.

Comprehensive Solving Techniques

1. Factoring Method: Factoring is often the most straightforward approach. It involves breaking down the quadratic into a product of binomials. In this case, finding two numbers that multiply to 28 (the constant term) and add up to -11 (the coefficient of $$) leads to the factors  $(x-4)$ and $$. Setting each factor equal to zero, we find the solutions: $x=4$ and $$.

2. Quadratic Formula: The quadratic formula, $x=\frac{-b\pm \sqrt{b^2-4\mathrm{ac}}}{2a}$, is a universal solver for quadratic equations. Applying it to our equation, we calculate $\mathrm{ x}=\frac{11\pm \sqrt{(-11{)}^2-4\cdot 1\cdot 28}}{2\cdot 1}$, leading to the same roots of  $$ and $$.

3. Completing the Square: This method involves rearranging the equation into a perfect square plus a constant. It’s a bit more complex but offers a deeper understanding of the equation’s geometry. For x2-11x+28=0, this method also confirms the roots found by the other methods.

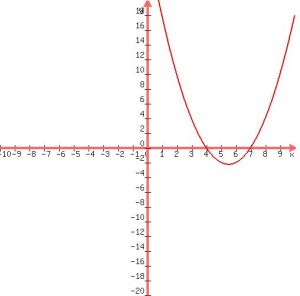
Graphical Insights

Plotting  x2−11x+28=0 reveals a parabola opening upwards. This orientation is due to the positive coefficient of x${}^2$. The vertex of the parabola provides the equation’s minimum value, and the roots (where the parabola crosses the x-axis) at $x=4$ and $x=7$ are key to understanding the equation’s real-world implications.

Diverse Applications

Quadratic equations are incredibly versatile:

• Physics: They model trajectories in projectile motion and the behavior of objects under uniform acceleration.
• Economics: Quadratics can represent various economic behaviors, like the relationship between supply, demand, and pricing.
• Engineering and Architecture: They assist in designing structures with specific stress and load requirements, like arches and bridges, using parabolic curves for optimal strength.

Also Read:

• Descending order meaning in Hindi
• x*x*x is equal to 2

Conclusion

The equation ${}^{}$ is more than just a mathematical problem; it’s a gateway to understanding a range of natural and man-made phenomena. By dissecting this equation, we uncover fundamental principles that apply across numerous fields, demonstrating the universal language of mathematics.

FAQs